How To Find Km And Vmax From Data

The effect of substrate concentration on enzyme activity

Skip the theory and get straight to: How to determine Km and Vmax

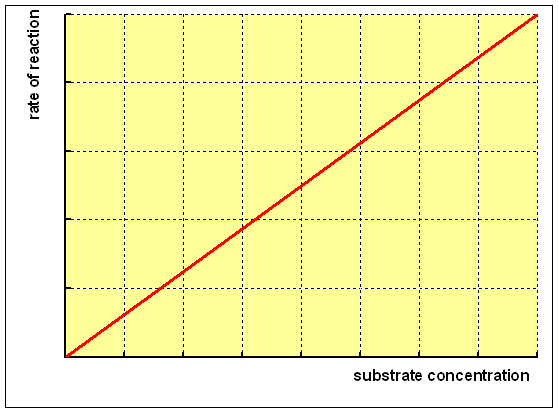
A simple chemic reaction with a unmarried substrate shows a linear relationship between the rate of formation of product and the concentration of substrate, as shown beneath:

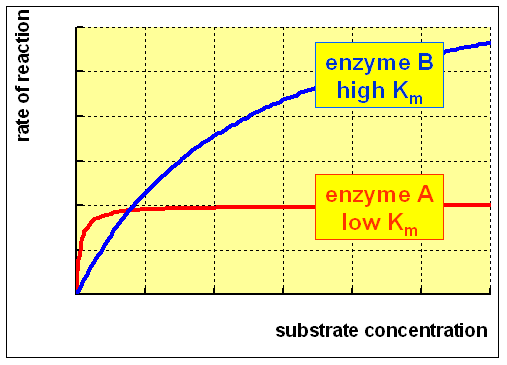
For an enzyme-catalysed reaction, in that location is usually a hyperbolic human relationship betwixt the charge per unit of reaction and the concentration of substrate, every bit shown below:

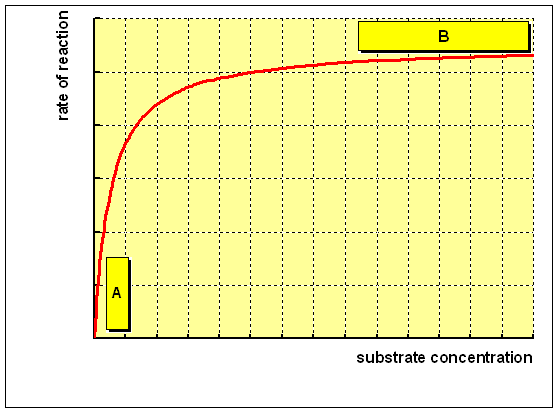
(A) At low concentration of substrate, at that place is a steep increase in the rate of reaction with increasing substrate concentration. The catalytic site of the enzyme is empty, waiting for substrate to bind, for much of the time, and the rate at which production can be formed is limited by the concentration of substrate which is available.

(B) As the concentration of substrate increases, the enzyme becomes saturated with substrate. Equally presently as the catalytic site is empty, more than substrate is bachelor to bind and undergo reaction. The charge per unit of germination of product now depends on the activity of the enzyme itself, and calculation more substrate will not affect the rate of the reaction to whatsoever meaning result.

The rate of reaction when the enzyme is saturated with substrate is the maximum rate of reaction, Vmax.
The relationship between charge per unit of reaction and concentration of substrate depends on the affinity of the enzyme for its substrate. This is usually expressed every bit the Km (Michaelis abiding) of the enzyme, an inverse mensurate of affinity.

For practical purposes, Km is the concentration of substrate which permits the enzyme to achieve half Vmax. An enzyme with a high Km has a depression affinity for its substrate, and requires a greater concentration of substrate to achieve Vmax."

The importance of determining Km and Vmax

The Km of an enzyme, relative to the concentration of its substrate under normal conditions permits prediction of whether or non the rate of formation of product will be affected by the availability of substrate.

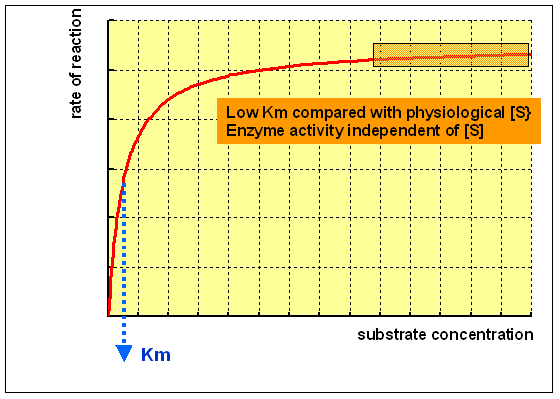
An enzyme with a low Km relative to the physiological concentration of substrate, as shown above, is normally saturated with substrate, and will deed at a more or less abiding charge per unit, regardless of variations in the concentration of substrate within the physiological range.

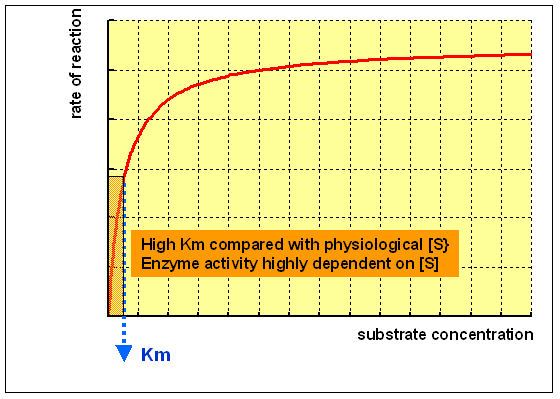
An enzyme with a loftier Km relative to the physiological concentration of substrate, as shown above, is not normally saturated with substrate, and its activity will vary as the concentration of substrate varies, so that the rate of formation of production will depend on the availability of substrate.

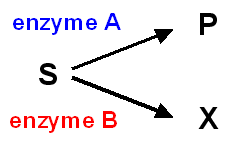If two enzymes, in different pathways, compete for the aforementioned substrate, then knowing the values of Km and Vmax for both enzymes permits prediction of the metabolic fate of the substrate and the relative amount that will menses through each pathway under diverse conditions.

In order to determine the amount of an enzyme present in a sample of tissue, it is obviously essential to ensure that the limiting factor is the activity of the enzyme itself, and not the corporeality of substrate bachelor. This means that the concentration of substrate must be high plenty to ensure that the enzyme is interim at Vmax. In practice, it is usual to utilize a concentration of substrate about 10 - 20-fold higher than the Km in order to determine the activeness of an enzyme in a sample.

If an enzyme is to be used to decide the concentration of substrate in a sample (e.g. glucose oxidase is used to measure out plasma glucose), then the substrate must be the limiting factor, and the concentration of substrate must exist beneath Km, so that the rate of formation of production increases steeply with increasing concentration of substrate, so providing a sensitive assay for the substrate."

How to determine Km and Vmax

Km and Vmax are determined by incubating the enzyme with varying concentrations of substrate; the results tin be plotted as a graph of rate of reaction (v) against concentration of substrate ([South], and will normally yield a hyperbolic curve, as shown in the graphs in a higher place.
The relationship is defined by the Michaelis-Menten equation:

v = Vmax / (i + (Km/[S]))

I t is difficult to fit the best hyperbola through the experimental points, and difficult to determine Vmax with whatever precision past estimating the limit of the hyperbola at infinite substrate concentration. A number of means of re-arranging the Michaelis-Menten equation take been devised to obtain linear relationships which permit more precise plumbing fixtures to the experimental points, and interpretation of the values of Km and Vmax. There are advantages and disadvantages associated with all three main methods of linearising the information.

The Lineweaver-Burk double reciprocal plot rearranges the Michaelis-Menten equation as:

1 / v = ane / Vmax + Km / Vmax 10 i / [South]

plotting 1/v against i/[S] give a straight line:

y intercept = 1 / Vmax
gradient = Km / Vmax
x intercept = -1/ Km

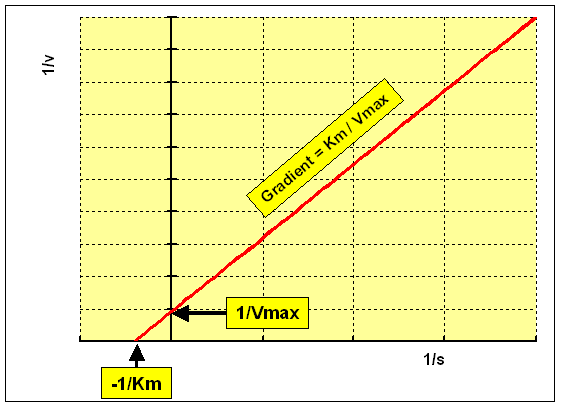
This is the most widely used method of linearising the data, and more often than not gives the best precision for estimates of Km and Vmax. Still, it has the disadvantage of placing undue weight on the points obtained at low concentrations of substrate (the highest values of ane/[Due south] and 1/v). These are the points at which the precision of determining the rate of reaction is lowest, considering the smallest corporeality of production has been formed.

The Eadie-Hofstee plot rearranges the Michaelis-Menten equation as:

v = Vmax - Km ten five / [S]

plotting v against 5 / [S] gives a straight line:

y intercept = Vmax
slope = -Km
10 intercept = Vmax / Km

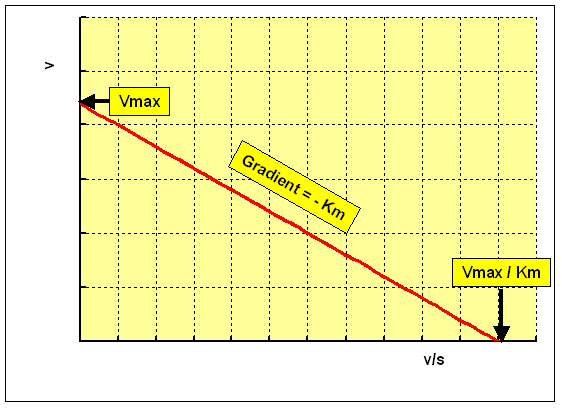
This plot overcomes the problem of uneven spacing of points, and undue weight given to points at low concentrations of substrate. However, it has the disadvantage that v, which is a dependent variable, is used on both axes, and hence errors in measuring the rate of reaction are multiplied, resulting in lower precision of the estimates of Km and Vmax

The Hanes plot rearranges the Michaelis-Menten equation as:

[S] / v = Km / Vmax + [S] / Vmax

plotting [S] / 5 against [S] gives a straight line:

y intercept = Km / Vmax
slope = ane / Vmax
ten intercept = -Km

This plot overcomes the problem of uneven spacing of points, and undue weight given to points at low concentrations of substrate. However, it has the disadvantage that [South] is used on both axes, and hence pipetting errors, which lead to errors in the true concentration of substrate available, are multiplied, resulting in lower precision of the estimates of Km and Vmax.